This is the first post of a series of notes on reinforcement learning. The aim for this series is to document my understanding of RL and provide a minimal level of knowledge (but with reasonable amount of mathematical rigor) for engineers to get started with RL.

1. The Goal of Reinforcement Learning

The goal is to learn a policy ${\pi }_{\theta }({\mathbf{a}}_t|{\mathbf{s}}_t)$ that maximizes the expected return $J(\theta )$.

Where $\tau$ is a trajectory $({\mathbf{s}}_1,{\mathbf{a}}_1,\dots ,{\mathbf{s}}_T,{\mathbf{a}}_T)$ and $p_{\theta }(\tau )$ is the probability of the trajectory under policy ${\pi }_{\theta }$:

Where the notation is defined as follows:

• ${\mathbf{s}}_t$: State at time step $t$.
• ${\mathbf{a}}_t$: Action at time step $t$.
• $r({\mathbf{s}}_t,{\mathbf{a}}_t)$: Reward function.
• ${\pi }_{\theta }({\mathbf{a}}_t|{\mathbf{s}}_t)$: Policy with parameters $\theta$.
• $p({\mathbf{s}}_{t+1}|{\mathbf{s}}_t,{\mathbf{a}}_t)$: Transition dynamics of the environment.
• $p({\mathbf{s}}_1)$: Initial state distribution.
• $\tau$: A trajectory sequence $\{{\mathbf{s}}_1,{\mathbf{a}}_1,\dots ,{\mathbf{s}}_T,{\mathbf{a}}_T\}$.
• $p_{\theta }(\tau )$: Probability of observing trajectory $\tau$ under policy $\theta$.
• $r(\tau )$: Cumulative return of trajectory $\tau$.

The following diagram illustrates the relationship between these variables in a Markov Decision Process (MDP):

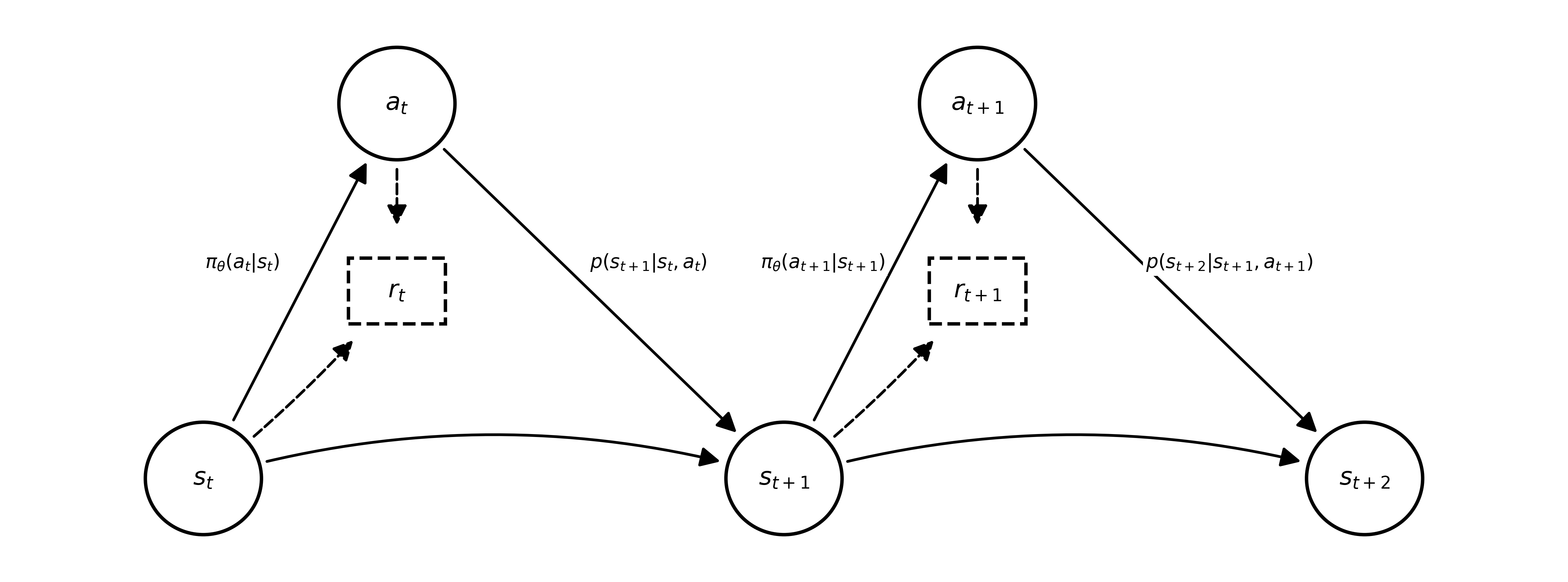
2. The Policy Gradient

We want to update $\theta$ in the policy with ${\nabla }_{\theta }J(\theta )$. Using the log-derivative trick: ${\nabla }_{\theta }{p}_{\theta }(\tau )=p_{\theta }(\tau ){\nabla }_{\theta }\log p_{\theta }(\tau )$, we get:

Expanding $\log p_{\theta }(\tau )$, the terms involving the dynamics $p({\mathbf{s}}_{t+1}|{\mathbf{s}}_t,{\mathbf{a}}_t)$ do not depend on $\theta$, so their gradient is zero. We are left with:

Interpretation

This equation decomposes the gradient into two parts:

1. Policy Direction: $\sum {\nabla }_{\theta }\log {\pi }_{\theta }({\mathbf{a}}_t|{\mathbf{s}}_t)$ represents the direction in parameter space that increases the probability of the actions taken in the trajectory.
2. Trajectory Reweighting: $\sum r({\mathbf{s}}_t,{\mathbf{a}}_t)$ acts as a scalar weight.

The gradient update pushes the policy parameters $\theta$ in the direction of trajectories that yield high cumulative rewards ("trial and error"). Formally, it scales the gradient of the log-probability of the trajectory by its return.

The REINFORCE Algorithm

The REINFORCE algorithm (Williams, 1992) is the simplest implementation of the policy gradient. It uses Monte Carlo sampling to estimate the return $r(\tau )$.

Since it relies on the full trajectory return (Monte Carlo), REINFORCE is unbiased but suffers from high variance, often leading to slow convergence.

Why is variance high?

1. Stochasticity: In a standard MDP, both the policy and the environment are stochastic. A single sampled trajectory is just one realization of a highly variable process. High-probability paths might yield low rewards due to a few unlucky transitions, and vice-versa.
2. Difficulty in Credit Assignment: REINFORCE uses the total return $G_t$ to update all actions in the trajectory. If a trajectory has a high return, the algorithm reinforces every action taken, even if some were suboptimal. Without a critic to evaluate individual states, the signal ("good" or "bad") is smeared across the entire sequence, introducing significant noise.
3. Magnitude of Returns: The gradient updates are scaled by the return $G_t$. If returns vary wildly in magnitude (e.g., one path gives 0, another gives 1000), the gradient updates will swing violently, destabilizing the learning process.

3. Variance Reduction

The standard policy gradient estimator has high variance. We can reduce this variance using two main techniques: Causality and Baselines.

3.1 Exploiting Causality (Reward-to-Go)

The policy at time $t$ cannot affect rewards obtained in the past ($t^{\prime }<t$). Therefore, we can replace the total return with the reward-to-go:

The term ${\sum }_{t^{\prime }=t}^{T}r({\mathbf{s}}_{i,t^{\prime }},{\mathbf{a}}_{i,t^{\prime }})$ is often denoted as ${\hat{Q}}_{i,t}$.

3.2 Baselines

We can subtract a baseline $b({\mathbf{s}}_t)$ from the return without introducing bias, as long as the baseline does not depend on the action ${\mathbf{a}}_t$:

Thus, the policy gradient with a baseline is:

A common choice for the baseline is the average reward or a learned Value Function $V_{\varphi }({\mathbf{s}}_t)$. This significantly reduces variance.

4. Implementation

In automatic differentiation frameworks (like PyTorch or TensorFlow), we don't compute the gradient manually. Instead, we construct a "surrogate loss" whose gradient equals the policy gradient.

Where ${\hat{A}}_{i,t}$ is the estimated advantage (e.g., ${\hat{Q}}_{i,t}-b({\mathbf{s}}_{i,t})$). We treat ${\hat{A}}_{i,t}$ as a fixed constant (detach from graph) during backpropagation.

Algorithm:

1. Sample: Run policy ${\pi }_{\theta }$ to collect trajectories $\{{\tau }_i\}$.
2. Estimate Return: Compute reward-to-go ${\hat{Q}}_{i,t}$ and optionally fit a baseline $V_{\varphi }$.
3. Update: Compute gradient ${\nabla }_{\theta }J$ and update $\theta \leftarrow \theta +\alpha {\nabla }_{\theta }J$.

Suggested Readings

• Williams (1992): Simple statistical gradient-following algorithms (REINFORCE).
• Sutton et al. (2000): Policy Gradient Theorem.
• Schulman et al. (2015): Trust Region Policy Optimization (TRPO).