This is a learning note to summarize the CS336 LM from Scratch course (opens in a new tab). I will provde minimal level background knowledge for each topic and implementation for each component.

1. Tokenization: Byte-Pair Encoding (BPE)

Before a model can process text, raw strings must be converted into sequences of integers.

1.1 Why UTF-8? (The Foundation)

The Challenge:

• Characters are complex: There are >150,000 Unicode characters. A vocabulary of this size is too large.
• Bytes are simple: There are only 256 unique bytes. This is a manageable base vocabulary.

1.2 The "Goldilocks" Problem

There is a trade-off in how we split text:

• Character/Byte-level: Vocabulary is small (256), but sequences become incredibly long, making attention computationally expensive (quadratic cost).
• Word-level: Sequences are short, but the vocabulary becomes massive and sparse, leading to many "Unknown" (UNK) tokens.

1.3 The Solution: BPE

Byte-Pair Encoding (BPE) is the standard "middle ground" used by models like GPT-2, Llama, and modern Frontier models.

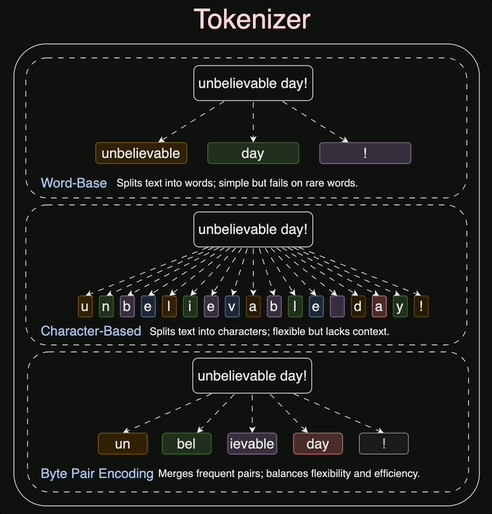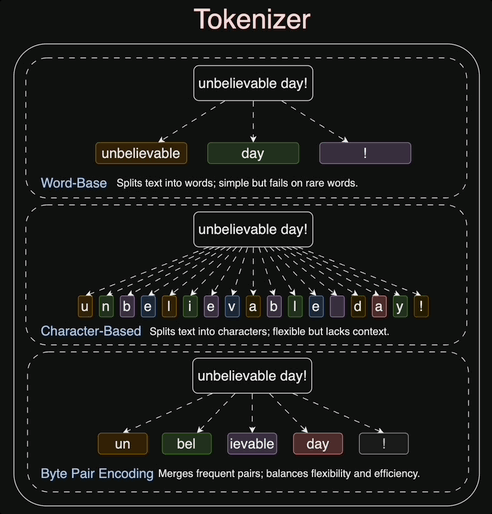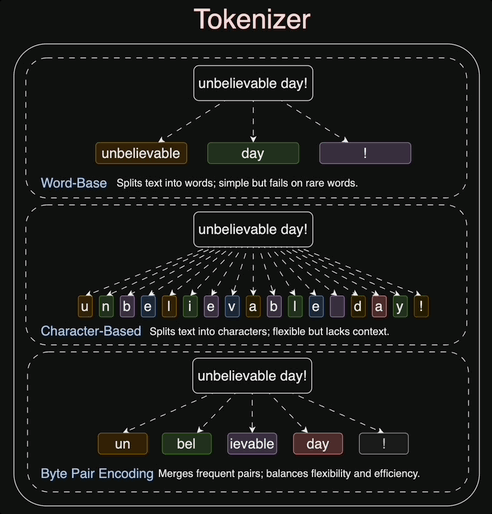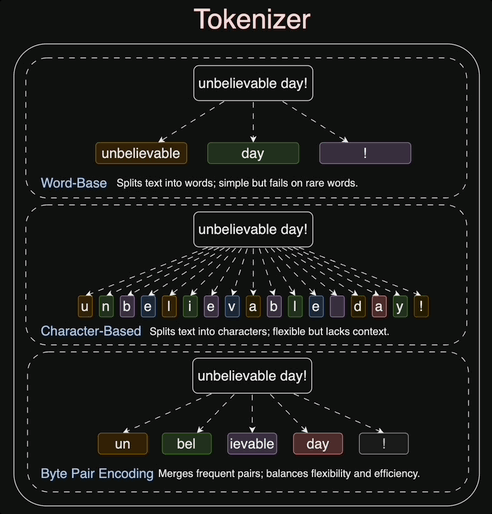
The Greedy Logic:

1. Count all adjacent pairs of tokens in the corpus.
2. Pick the single most frequent pair.
3. Merge it into a new token.
4. Repeat.

Reusing Vocabulary:

• Start with t, h, e
• Merge t+h -> th
• Merge th+e -> the
• Result: Vocabulary contains t, h, e, th, AND the

Tie-Breaking: If two pairs have the same frequency, pick the lexicographically larger one.

1.4 Implementation

def train_bpe(string: str, num_merges: int) -> BPETokenizerParams:
    # Start with the list of bytes of string.
    indices = list(map(int, string.encode("utf-8")))
    merges: dict[tuple[int, int], int] = {}  # index1, index2 => merged index
    vocab: dict[int, bytes] = {x: bytes([x]) for x in range(256)}
 
    for i in range(num_merges):
        # Count occurrences of each pair of tokens
        counts = defaultdict(int)
        for index1, index2 in zip(indices, indices[1:]):
            counts[(index1, index2)] += 1
        
        if not counts:
            break
 
        # Find the most common pair.
        pair = max(counts, key=counts.get)
        index1, index2 = pair
 
        # Merge that pair.
        new_index = 256 + i
        merges[pair] = new_index
        vocab[new_index] = vocab[index1] + vocab[index2]
        indices = merge(indices, pair, new_index)
 
    return BPETokenizerParams(vocab=vocab, merges=merges)

A full self-contained implementation can be found in train_bpe.py (opens in a new tab).

1.5 The Encoding Process (Deterministic Replay)

How does BPE tokenize a new string? It does not search for the longest match. It replays the training history.

The Rule: Encoding means iterating through the merges dict (not vocab) in order. For each merge (a, b) -> c, check if a is adjacent to b in the current sequence. If yes, replace them with c.

merges vs vocab:

• merges: {(t, h): 256, (th, e): 257, ...} — Used during encoding to know which pairs to merge.
• vocab: {256: b'th', 257: b'the', ...} — Used during decoding to convert tokens back to bytes.

Example 1: Assume merge order: (1) t+h->th, (2) th+e->the

1. Input: [t, h, e]
2. Check Merge #1: Is (t, h) in merges AND adjacent? Yes -> [th, e]
3. Check Merge #2: Is (th, e) in merges AND adjacent? Yes -> [the]

Example 2 (Different merge order): Assume: (1) h+e->he, (2) t+h->th

1. Input: [t, h, e]
2. Check Merge #1: Is (h, e) in merges AND adjacent? Yes -> [t, he]
3. Check Merge #2: Is (t, h) in merges AND adjacent? No (h was consumed) -> [t, he]

The final tokenization depends strictly on the merge order, not which subword is "longest."

• Byte-Level BPE: We encode text into UTF-8 bytes (opens in a new tab) first. This ensures the base vocabulary is always size 256, and every possible string can be encoded without UNK tokens.
• Special Tokens: Control tokens like <|endoftext> are added to the vocabulary manually and prevented from being merged with regular text during BPE training.

UTF-8 Prefix Code Guarantee: UTF-8 is a variable-width encoding that guarantees unique, unambiguous decoding using bit prefixes.

UTF-8 Byte Type Reference:

Byte Type	Binary Prefix	Meaning
ASCII	0xxxxxxx	A standalone character (e.g., a, 9).
Start Byte	110xxxxx	Start of a 2-byte character.
Start Byte	1110xxxx	Start of a 3-byte character (e.g., Japanese).
Continuation	10xxxxxx	Part of a sequence; never a start.