What is autodecoder?
Autodecoder
Introduction
The auto-encoder is widely used in machine learning area and become an tool of great importance in dealing embedding and generative tasks. However, in most AE based generative model, the encoder isn’t of any use. Is it possible to get rid of the encoder in the first place and just train a decoder? With this question, I summarized some exploration in related literature.
What is auto-decoder?
An auto-decoder is used for decoding embedding to useful targets like images, videos, texts and etc. Unlike auto-encoder, auto-decoder does not have encoder part. A comparison of two model architectures is shown in figure.
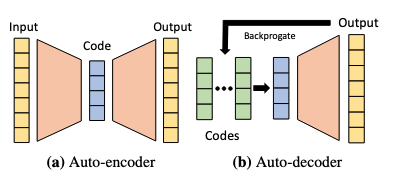
What is the setup of auto-decoder?
The goal of this model is to decode an embeded information \(z_i\in\mathrm{R}^d\)(latent space) into meaning for information \(x_i\in\mathrm{R}^n\)(“physical space”). The model decodes as \(x_i\approx f_\theta(z_i)\), where \(\theta\) is learnable model parameters.
How to train a auto-decoder?
There are two parts are trainable:
- The model parameters \(\theta\)
- The embeddings \(z_i\)s
Both \(z_i\)’s and \(\theta\) are randomly initialized and trained according to the following loss function: \(\begin{equation}\label{eq:auto_decode_loss} \text{argmin}_{\theta,\{z_i\}}\sum_{i=1}^N\left(\mathcal{L}(f_\theta(z_i), x_i)+\frac{1}{\sigma^2}\|z_i\|^2\right). \end{equation}\)
Can we encode information(text, image etc) with auto-decoder?
Yes, but not as in auto-encoder. Since there is no encoder part in the auto-decoder architecture, the computation of an embedding is more nontrivial. When a auto-decoder is trained, for a given information \(x\), you can randomly initialize an embedding \(z\). Then, optimize \(z\) through the Eq.(\(\ref{eq:auto_decode_loss}\)), with model parameters \(\theta\) fixed.
Auto-decoder in pactice
In this example, let’s use \(\{x_i(t)\}\) be a set of functions and \(\{z_i\}\) be their embeddings. In this case, the auto-decoder maps an embedding \(z_i\) to a function \(x_i(t)\).
Setup
For each function \(x_i(t)\), we randomly sample K sample points \(\{(t_k, x_i(t_k))\}_{i=1}^K\). The loss function is
\[\begin{equation} \text{argmin}_{\theta,\{z_i\}}\sum_{i=1}^N\sum_{k=1}^K\left(\mathcal{L}(f_\theta(z_i, t_k), x_i(t_k))+\frac{1}{\sigma^2}\|z_i\|^2\right). \end{equation}\]How does the optimization process work?
As we are optimising two sets of variables (the network weights and the latent vectors), we need to choose an optimisation strategy. The original paper does not detail how they optimised their objective function. In this implementation, we will alternate the optimisation of the latent vectors first for 20 epochs, and then the model parameters for 20 epochs. We do this 20 times, and we call this an alternating optimisation strategy. Alternatively, one can also optimize in a single process by using a single optimizer for both set of parameters. In both cases, we randomly sample minibatch \(B\) examples from \(N\times K\) data points.